Slider crank example#
This notebook is an exmaple of a simple slider crank. This demonstrates how to do the following:
Requirements:
In this tutorial we will:
Create a Multibody using DataStruct.DataStruct
Use ConstraintKinematicsSolver solve a system
Setup the simulation
Run the simulation with constraints
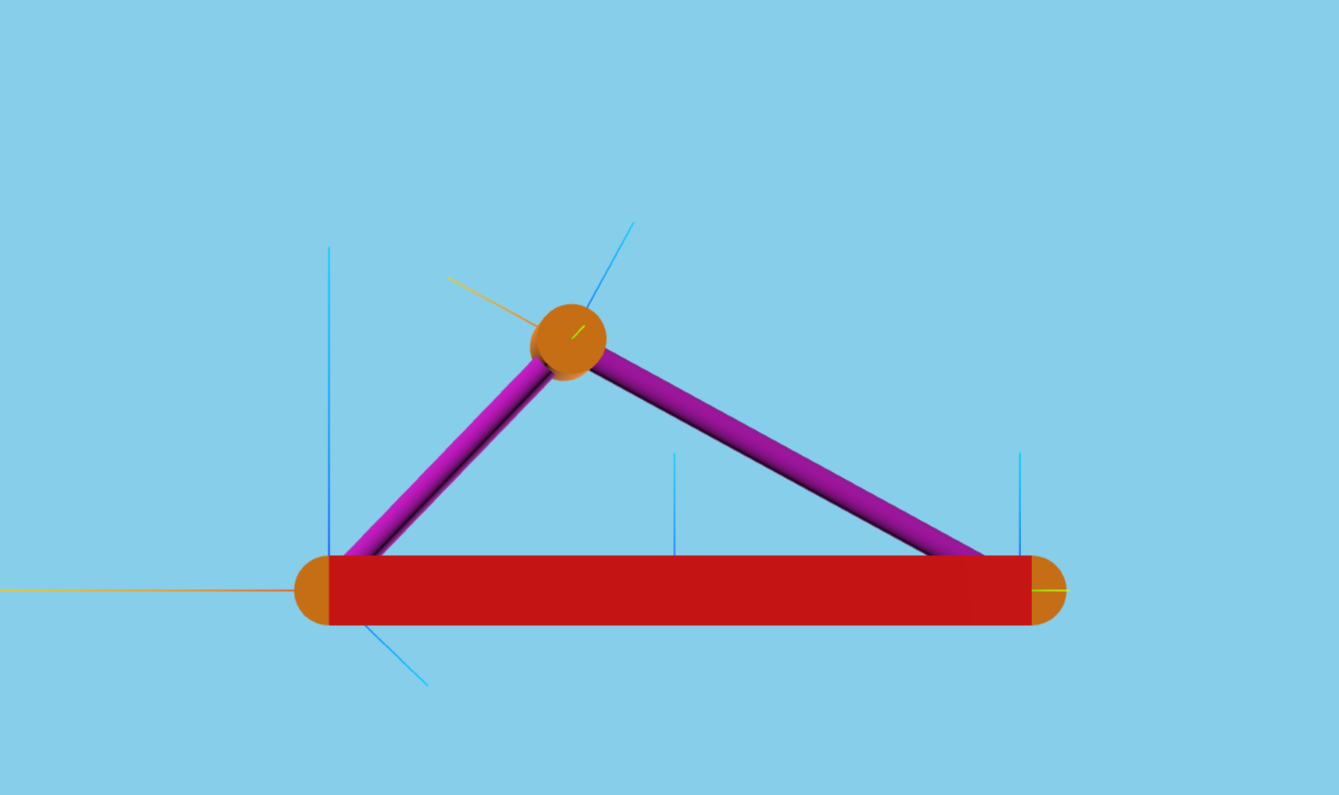
For a more in-depth descriptions of kdflex concepts see usage.
import numpy as np
import atexit
from copy import deepcopy
from typing import cast
from Karana.Core import discard, allFinalized
from Karana.Frame import FrameContainer
from Karana.Math import IntegratorType
import quantities as pq
from Karana.Dynamics import (
HINGE_TYPE,
StatePropagator,
SPSOLVER_TYPE,
TimedEvent,
PhysicalBody,
)
from Karana.Dynamics.SOADyn_types import (
BodyDS,
HingeDS,
PinSubhingeDS,
BodyWithContextDS,
MultibodyDS,
LoopConstraintHingeDS,
LinearSubhingeDS,
ConstraintFrameDS,
NodeDS,
)
from Karana.Math import UnitQuaternion
from Karana.Models import UpdateProxyScene, SyncRealTime
Create a Multibody Using DataStruct#
Let’s create the slider-crank multibody. Here, we choose to do so via DataStruct.DataStruct s. We define a DataStruct for each body, and then combine them together into a SOADyn_types.MultibodyDS.
DataStructs have support for units. The units will be automatically converted to the simulation’s units system, which is SI units by default. The link_1 BodyDS has an example of this, where the mass units are in lbs.
fc = FrameContainer("root")
# Create a BodyDS for the first link. This can be used to specify all the parameters for the body, and the way
# the body attaches to it's parent, i.e., the hinge.
link_1 = BodyDS(
name="link_1",
mass=1.0 * pq.lb,
b2cm=np.zeros(3),
inertia=np.eye(3),
hinge=HingeDS(
hinge_type=HINGE_TYPE.PIN,
subhinges=[
PinSubhingeDS(prescribed=False, unit_axis=np.array([0.0, 1.0, 0.0]))
], # pyright: ignore - Types are okay
),
body_to_joint=np.array([-0.25, 0.0, 0.0]),
)
# Let's create the second link of our slider crank. Here, we will simply copy the first and modify the parameters
# that should be changed.
link_2 = deepcopy(link_1)
link_2.name = "link_2"
link_2.mass = 2.0 * pq.kg
link_2.body_to_joint = np.array([0.75, 0.0, 0.0])
link_2.inb_to_joint = np.array([0.25, 0.0, 0.0])
# We create a block body in a similar fashion. The block is the body that will have the slider constraint,
# so we also add a constraint node via a NodeDS.
block = deepcopy(link_1)
block.name = "block"
block.mass = 1.0
block.body_to_joint = np.zeros(3)
block.constraint_nodes = [
NodeDS(
name="cn",
constraint_node=True,
force_node=True,
)
]
# Now, we combine all the bodies together to form a MultibodyDS. In addition, we add our LoopConstraint
# and a constraint frame for the slider constraint.
mbody_ds = MultibodyDS(
name="mb",
base_bodies=[
BodyWithContextDS(
body=link_1,
children=[
BodyWithContextDS(
body=link_2,
children=[
BodyWithContextDS(body=block, children=[]),
],
),
],
)
],
loop_constraints=[
LoopConstraintHingeDS(
name="block_constraint",
hinge=HingeDS(
hinge_type=HINGE_TYPE.SLIDER,
subhinges=[LinearSubhingeDS(prescribed=False, unit_axis=np.array([1.0, 0.0, 0.0]))],
),
get_oframe={"frame": "constraint_frame"},
get_pframe={"body": "block", "node": "cn"},
)
],
constraint_frames=[
ConstraintFrameDS(
name="constraint_frame",
translation=np.zeros(3),
unit_quaternion=UnitQuaternion(0, 0, 0, 1),
parent="newtonian",
)
],
)
DataStructs can be saved to a varity of formats, for example YAML and HDF5. This makes it easy to re-create the same DataStruct in different simulations.
Here, we don’t need to save the DataStruct for later, we simply use it to create the Multibody.
# Create the Multibody from the DataStruct
mb = mbody_ds.toMultibody(fc)
del mbody_ds, link_2, block
# Once all bodies are created, we make the Multibody current. This sets up internal
# varibles for use in dynamics computations.
mb.ensureCurrent()
As mentioned previously, values are automatically converted to the correct units system.
print(f"DataStruct value for link_1 mass: {link_1.mass}")
link_1_bd = cast(PhysicalBody, mb.getBody("link_1"))
print(f"Mass for link_1 in the multibody: {link_1_bd.getSpatialInertia().mass()} kg")
del link_1_bd, link_1
DataStruct value for link_1 mass: 1.0 lb
Mass for link_1 in the multibody: 0.45359237 kg
Use ConstraintKinematicsSolver to Solve the System#
Now, we initialize the state with the Karana.Dynamics.ConstraintKinematicsSolver
# Now, we need to initialize our state. Our state has constraints, so we will use the
# ConstraintKinematicsSolver to get a valid state that satisfies the constraints.
# First, we set everything to zero as our initial guess, except the velocity of the
# first link. We want this to have an initial velocity so that our slider-crank moves.
cd = mb.subhingeCoordData()
cd.setQ(0.0)
cd.setU(0.0)
u = cd.getU()
u[0] = 1.0
cd.setU(u)
cd.setUdot(0.0)
cd.setT(0.0)
# In addition to the subhinge data, we also need to set the constraint data. We do so here.
cdc = mb.constraintCoordData()
cdc.setQ(0.0)
cdc.setU(0.0)
cdc.setUdot(0.0)
cdc.setT(0.0)
del cdc
The Karana.Dynamics.ConstraintKinematicsSolver has solveQ and solveU methods we will use. These methods return the error after solving. We will ensure this is less than 1e-6 before moving forward.
# Now, we create a ConstraintKinematicsSolver and solve for the initial state.
cks = mb.cks()
errQ = cks.solveQ()
errU = cks.solveU()
# Make sure we were able to solve for Q and U
assert abs(errQ) < 1e-6
assert abs(errU) < 1e-6
del cks
# Before we finalize everything (see below), we need to set the gravity. Ultimately, we will
# be setting this with a model (see further below). For now, we will just set this to zero
# so we can do the finalized check.
mb.setUniformGravAccel(np.zeros(3))
# verify the multibody and its state
assert allFinalized()
Setup the Simulation#
Start by calling the setupGraphics helper method on the multibody. This method takes care of setting up the graphics environment.
See Visualization and SceneLayer for more information relating to this section.
# setup graphics helper function
cleanup_graphics, web_scene = mb.setupGraphics(port=0, axes=0.5)
mb.createStickParts()
# position the viewpoint camera of the visualization
web_scene.defaultCamera().pointCameraAt([0, 3, 0], [0, 0, 0], [0, 0, 1])
del web_scene
[WebUI] Listening at http://newton:40443
Setup the Karana.Dynamics.StatePropagator and integrator.
# Set up state propagator and select integrator type: rk4 or cvode
sp = StatePropagator(
mb,
integrator_type=IntegratorType.RK4,
integ_opts=None,
solver_type=SPSOLVER_TYPE.TREE_AUGMENTED_DYNAMICS,
)
integrator = sp.getIntegrator()
sp_opts = sp.getOptions()
# Makes sure the visualization scene is updated after each state change.
UpdateProxyScene("update_proxy_scene", sp, mb.getScene())
# sync the simulation time with real-time.
SyncRealTime("sync_real_time", sp, 1.0)
# register callback to print the state at each step
f2f = fc.root().frame2Frame(mb.getBody("block"))
def post_step_fn(t, x):
print(
f"t = {float(integrator.getTime())/1e9}s; block_pos = {f2f.relTransform().getTranslation()}"
)
sp_opts.fns.post_hop_fns["update_and_info"] = post_step_fn
Initialize integrator state and add timed event
# Initialize integrator state
t_init = np.timedelta64(0, "ns")
sp.setTime(t_init)
sp.setState(mb.dynamicsToState())
# Syncs up graphics
mb.getScene().update()
# register the timed event
h = np.timedelta64(int(1e8), "ns")
t = TimedEvent("hop_size", h, lambda _: None, False)
t.period = h
sp.registerTimedEvent(t)
del t
Run the Simulation With Constraints#
Now, run the simualtion for 10 seconds. This will print the time and location of the block. The block should osscilate back and forth along the x-axis. The y- and z-components should be near zero, but may not be identically zero, because the slider is enforced via a constraint.
# run the simulation
print(f"t = {float(integrator.getTime())/1e9}s; x = {integrator.getX()}")
# run the simulation
sp.advanceTo(10.0)
# dump the state propagator info
sp.dump("sp")
t = 0.0s; x = [ 0. 0. 0. -0.25 1. -0.33333333
-0.66666667 0. ]
t = 0.1s; block_pos = [-2.50835263e-01 0.00000000e+00 2.66120017e-08]
t = 0.2s; block_pos = [-2.53364350e-01 0.00000000e+00 5.41549326e-08]
t = 0.3s; block_pos = [-2.57658048e-01 0.00000000e+00 8.36652793e-08]
t = 0.4s; block_pos = [-2.63837196e-01 0.00000000e+00 1.15819022e-07]
t = 0.5s; block_pos = [-2.72076493e-01 0.00000000e+00 1.50486238e-07]
t = 0.6s; block_pos = [-2.82608535e-01 0.00000000e+00 1.85912595e-07]
t = 0.7s; block_pos = [-2.95725945e-01 0.00000000e+00 2.17486330e-07]
t = 0.8s; block_pos = [-3.11777550e-01 0.00000000e+00 2.36557962e-07]
t = 0.9s; block_pos = [-3.31151907e-01 0.00000000e+00 2.31129365e-07]
t = 1.0s; block_pos = [-3.54239340e-01 0.00000000e+00 1.92102924e-07]
t = 1.1s; block_pos = [-3.81365729e-01 0.00000000e+00 1.27370642e-07]
t = 1.2s; block_pos = [-4.12703553e-01 0.00000000e+00 7.38739071e-08]
t = 1.3s; block_pos = [-4.48188762e-01 0.00000000e+00 8.23730407e-08]
t = 1.4s; block_pos = [-4.87488836e-01 0.00000000e+00 1.72212803e-07]
t = 1.5s; block_pos = [-5.30049758e-01 0.00000000e+00 3.09150500e-07]
t = 1.6s; block_pos = [-5.75200703e-01 0.00000000e+00 4.39428533e-07]
t = 1.7s; block_pos = [-6.22262221e-01 0.00000000e+00 5.32065287e-07]
t = 1.8s; block_pos = [-6.70616564e-01 0.00000000e+00 5.85742556e-07]
t = 1.9s; block_pos = [-7.19733069e-01 0.00000000e+00 6.13435375e-07]
t = 2.0s; block_pos = [-7.69162683e-01 0.00000000e+00 6.28946852e-07]
t = 2.1s; block_pos = [-8.18518032e-01 0.00000000e+00 6.41799976e-07]
t = 2.2s; block_pos = [-8.67449397e-01 0.00000000e+00 6.57142545e-07]
t = 2.3s; block_pos = [-9.15620994e-01 0.00000000e+00 6.77132508e-07]
t = 2.4s; block_pos = [-9.62688431e-01 0.00000000e+00 7.02232464e-07]
t = 2.5s; block_pos = [-1.00827661e+00 0.00000000e+00 7.32054536e-07]
t = 2.6s; block_pos = [-1.05195695e+00 0.00000000e+00 7.65833100e-07]
t = 2.7s; block_pos = [-1.09322319e+00 0.00000000e+00 8.02703910e-07]
t = 2.8s; block_pos = [-1.13146638e+00 0.00000000e+00 8.42000555e-07]
t = 2.9s; block_pos = [-1.16595277e+00 0.00000000e+00 8.83831970e-07]
t = 3.0s; block_pos = [-1.19581384e+00 0.00000000e+00 9.30178900e-07]
t = 3.1s; block_pos = [-1.22006652e+00 0.00000000e+00 9.86196835e-07]
t = 3.2s; block_pos = [-1.23768881e+00 0.00000000e+00 1.05974510e-06]
t = 3.3s; block_pos = [-1.24776842e+00 0.00000000e+00 1.15584883e-06]
t = 3.4s; block_pos = [-1.24970291e+00 0.00000000e+00 1.26785947e-06]
t = 3.5s; block_pos = [-1.24336897e+00 0.00000000e+00 1.37749156e-06]
t = 3.6s; block_pos = [-1.22916088e+00 0.00000000e+00 1.46895060e-06]
t = 3.7s; block_pos = [-1.20787213e+00 0.00000000e+00 1.53971250e-06]
t = 3.8s; block_pos = [-1.18049646e+00 0.00000000e+00 1.59631597e-06]
t = 3.9s; block_pos = [-1.14804876e+00 0.00000000e+00 1.64571041e-06]
t = 4.0s; block_pos = [-1.11145619e+00 0.00000000e+00 1.69167256e-06]
t = 4.1s; block_pos = [-1.07151534e+00 0.00000000e+00 1.73531760e-06]
t = 4.2s; block_pos = [-1.02889097e+00 0.00000000e+00 1.77644273e-06]
t = 4.3s; block_pos = [-9.84134123e-01 0.00000000e+00 1.81440708e-06]
t = 4.4s; block_pos = [-9.37706458e-01 0.00000000e+00 1.84854887e-06]
t = 4.5s; block_pos = [-8.90005078e-01 0.00000000e+00 1.87842145e-06]
t = 4.6s; block_pos = [-8.41385914e-01 0.00000000e+00 1.90408227e-06]
t = 4.7s; block_pos = [-7.92186007e-01 0.00000000e+00 1.92661065e-06]
t = 4.8s; block_pos = [-7.42745712e-01 0.00000000e+00 1.94898329e-06]
t = 4.9s; block_pos = [-6.93431844e-01 0.00000000e+00 1.97726863e-06]
t = 5.0s; block_pos = [-6.44661829e-01 0.00000000e+00 2.02151789e-06]
t = 5.1s; block_pos = [-5.96926428e-01 0.00000000e+00 2.09438169e-06]
t = 5.2s; block_pos = [-5.50803674e-01 0.00000000e+00 2.20393968e-06]
t = 5.3s; block_pos = [-5.06950102e-01 0.00000000e+00 2.33951657e-06]
t = 5.4s; block_pos = [-4.66052276e-01 0.00000000e+00 2.46182169e-06]
t = 5.5s; block_pos = [-4.28733184e-01 0.00000000e+00 2.52148124e-06]
t = 5.6s; block_pos = [-3.95438954e-01 0.00000000e+00 2.50352447e-06]
t = 5.7s; block_pos = [-3.66359362e-01 0.00000000e+00 2.44386597e-06]
t = 5.8s; block_pos = [-3.41423812e-01 0.00000000e+00 2.39251089e-06]
t = 5.9s; block_pos = [-3.20366214e-01 0.00000000e+00 2.37500228e-06]
t = 6.0s; block_pos = [-3.02816295e-01 0.00000000e+00 2.38976466e-06]
t = 6.1s; block_pos = [-2.88378318e-01 0.00000000e+00 2.42412620e-06]
t = 6.2s; block_pos = [-2.76681813e-01 0.00000000e+00 2.46629842e-06]
t = 6.3s; block_pos = [-2.67406922e-01 0.00000000e+00 2.50905808e-06]
t = 6.4s; block_pos = [-2.60293115e-01 0.00000000e+00 2.54915934e-06]
t = 6.5s; block_pos = [-2.55139177e-01 0.00000000e+00 2.58580872e-06]
t = 6.6s; block_pos = [-2.51799701e-01 0.00000000e+00 2.61946151e-06]
t = 6.7s; block_pos = [-2.50180994e-01 0.00000000e+00 2.65111438e-06]
t = 6.8s; block_pos = [-2.50237855e-01 0.00000000e+00 2.68195172e-06]
t = 6.9s; block_pos = [-2.51971872e-01 0.00000000e+00 2.71317988e-06]
t = 7.0s; block_pos = [-2.55431489e-01 0.00000000e+00 2.74592070e-06]
t = 7.1s; block_pos = [-2.60713815e-01 0.00000000e+00 2.78105624e-06]
t = 7.2s; block_pos = [-2.67967937e-01 0.00000000e+00 2.81890799e-06]
t = 7.3s; block_pos = [-2.77399033e-01 0.00000000e+00 2.85860861e-06]
t = 7.4s; block_pos = [-2.89271757e-01 0.00000000e+00 2.89704924e-06]
t = 7.5s; block_pos = [-3.03909846e-01 0.00000000e+00 2.92755471e-06]
t = 7.6s; block_pos = [-3.21686555e-01 0.00000000e+00 2.93934978e-06]
t = 7.7s; block_pos = [-3.42997834e-01 0.00000000e+00 2.92068698e-06]
t = 7.8s; block_pos = [-3.68209642e-01 0.00000000e+00 2.86945263e-06]
t = 7.9s; block_pos = [-3.97577588e-01 0.00000000e+00 2.80866181e-06]
t = 8.0s; block_pos = [-4.31155962e-01 0.00000000e+00 2.78709020e-06]
t = 8.1s; block_pos = [-4.68736392e-01 0.00000000e+00 2.84451672e-06]
t = 8.2s; block_pos = [-5.09857422e-01 0.00000000e+00 2.97052659e-06]
t = 8.3s; block_pos = [-5.53888065e-01 0.00000000e+00 3.11402288e-06]
t = 8.4s; block_pos = [-6.00141274e-01 0.00000000e+00 3.23016801e-06]
t = 8.5s; block_pos = [-6.47964860e-01 0.00000000e+00 3.30509799e-06]
t = 8.6s; block_pos = [-6.9678682e-01 0.0000000e+00 3.3472802e-06]
t = 8.7s; block_pos = [-7.46122007e-01 0.00000000e+00 3.37124283e-06]
t = 8.8s; block_pos = [-7.95557218e-01 0.00000000e+00 3.38871488e-06]
t = 8.9s; block_pos = [-8.44728210e-01 0.00000000e+00 3.40674236e-06]
t = 9.0s; block_pos = [-8.93295579e-01 0.00000000e+00 3.42869198e-06]
t = 9.1s; block_pos = [-9.40921696e-01 0.00000000e+00 3.45568294e-06]
t = 9.2s; block_pos = [-9.87248538e-01 0.00000000e+00 3.48764580e-06]
t = 9.3s; block_pos = [-1.03187536e+00 0.00000000e+00 3.52394889e-06]
t = 9.4s; block_pos = [-1.07433518e+00 0.00000000e+00 3.56374347e-06]
t = 9.5s; block_pos = [-1.11406996e+00 0.00000000e+00 3.60622304e-06]
t = 9.6s; block_pos = [-1.15040639e+00 0.00000000e+00 3.65103377e-06]
t = 9.7s; block_pos = [-1.18253856e+00 0.00000000e+00 3.69911405e-06]
t = 9.8s; block_pos = [-1.20953137e+00 0.00000000e+00 3.75401755e-06]
t = 9.9s; block_pos = [-1.23036702e+00 0.00000000e+00 3.82265815e-06]
t = 10.0s; block_pos = [-1.24405911e+00 0.00000000e+00 3.91245475e-06]
sp |---> Dumping "sp" ({py:class}`Karana.Core.LockingBase`)
sp <Base> id=494
sp <Base> refCount=1
sp <LockingBase> isCurrent=true
sp <LockingBase> upstream deps:
sp <LockingBase> downstream deps:
sp Dumping StatePropagator: time=10s, nstates=8, integrator=RK4
sp pre hop fns:
sp Dumping functions in callback registry:
sp 0: sync_real_time_pre_hop
sp post hop fns:
sp Dumping functions in callback registry:
sp 0: update_proxy_scene_post_hop
sp 1: sync_real_time_post_hop
sp 2: update_and_info
sp Dumping scheduler: num_before_hop_timed_events 0, num_after_hop_timed_events 1
sp Before hop events:
sp After hop events:
sp Dumping TimedEvent hop_size
sp Has event set.
sp Next scheduled event time: 10100000000ns
sp This will run after the hop.
sp Will be rescheduled with a period of 100000000ns.
sp Has a priority of 0.
sp Counters: hops=100, derivs=400, integration steps=100, zero crossings=0
Below, we cleanup everything whenever the script exits. This requires us to delete local variables and discard our containers and scene.
def cleanup():
global integrator, sp_opts, cd
del integrator, sp_opts, cd
discard(sp)
cleanup_graphics()
discard(mb)
discard(fc)
atexit.register(cleanup)
<function __main__.cleanup()>
Summary#
You are now familiar with creating amultibody using DataStruct and setting up constraints for it using ConstraintKinematicsSolver. These constraints are automatically enforced when the simulation is run.
Further Readings#
Load a mars 2020 rover urdf
Load a robotic arm urdf
Enforce loop constraints in a double-wishbone model
Drive an ATRVjr rover